Die von Walther Nernst aufgestellte Gleichung kommt ursprünglich aus der Elektrochemie; mit ihr kann man die konzentrationsabhängige Spannung berechnen, die zwischen zwei galvanischen Halbzellen besteht. Leute, die Ahnung von Chemie, vor allem von Elektrochemie haben, können den folgenden Exkurs gerne überspringen und gleich zur Berechnung des Membranpotenzials springen.
Exkurs in die Elektrochemie
Eine Halbzelle besteht aus einer Elektrode, zum Beispiel Zink, und einem Elektrolyten, also einer salzhaltigen, elektrisch leitenden Lösung, die zur Elektrode passen muss. Für die Zink-Elektrode würde sich zum Beispiel eine Lösung von Zinkchlorid anbieten, für eine Kupfer-Elektrode eine Lösung aus Kupfersulfat.
Eine Standard-Halbzelle ist eine Halbzelle, bei der die Konzentration des Elektrolyten genau 1 mol/l beträgt.
Ein galvanisches Element erhält man, wenn man zwei Halbzellen miteinander verbindet. Verbindet man beispielsweise eine Zink-Halbzelle mit einer Kupferhalbzelle, kann man eine elektrische Spannung messen. Die Höhe dieser Spannung berechnet sich aus den Standard-Redoxpotenzialen der Halbzellen. Diese Redoxpotenziale kann man in Tabellen nachschauen. Für die Standard-Zinkhalbzelle beträgt das Redoxpotenzial -0,76 Volt, für die Standard-Kupferhalbzelle +0,35 Volt. Ein galvanisches Element, das aus zwei solchen Standard-Halbzellen besteht, liefert dann eine Spannung von 1,11 Volt. Das ist genau die Differenz zwischen den beiden Standard-Redoxpotenzialen von Zink und Kupfer.
Weitere Informationen zu Halbzellen und Galvanischen Elementen finden Sie auf meinen Chemieseiten unter "Die Spannungsreihe der Metalle".
Nun ist es oft aber so, dass bei einer Batterie oder einem Akkumulator oder bei anderen elektrochemischen Vorgängen keine Standard-Halbzellen mit 1-molaren Salzlösungen vorliegen. Meistens haben die Elektrolyten andere Konzentrationen, beispielsweise C(ZnSO4) = 0,35 mol/l und c(CuSO4) = 1,22 mol/l. Wie kann man nun die Spannung berechnen, die zwischen diesen beiden Halbzellen besteht? Dazu verwendet man folgende Gleichung, die nach Walther Nernst benannt wurde.
$U_{H} = U_{H}^{ \ 0} + \frac{0,059V}{z} * lg\frac{c(Me^{z+})}{mol/l}$Dabei ist $U_{H}^{ \ 0} $ das Standard-Redoxpotenzial der Halbzelle, 0,059 V ist eine Konstante, z ist die Zahl der Elektronen, die von dem Metall-Ionen aufgenommen werden kann (bei Kupfer oder Zink ist z = 2, bei Silber 1, bei Aluminium 3 und so weiter), und $c(Me^{z+})$ ist die Konzentration des Elektrolyten.
Spielen wir das einmal für die Kupferhalbzelle mit c(CuSO4) = 1,22 mol durch. Das Standard-Redoxpotenzial für die Kupferzelle ist +0,35 Volt.
$U_{H} = 0,35 V + \frac{0,059V}{2} * lg\frac{1,22 \ mol/l}{mol/l}$
$U_{H} = 0,35 V + \frac{0,059V}{2} * 0,086$
$U_{H} = 0,35 V + 0,0025 V= 0,3525 V$
Das Redoxpotenzial dieser Kupferhalbzelle ist also etwas größer (positiver) als das der Standard-Kupferhalbzelle. Das liegt daran, dass in Kupfer-Zink-Element das Kupfer die Rolle des Elektronen-Akzeptors spielt, also Elektronen aufnimmt:
$Cu^{2+}_{(aq)} + 2 e^{-} \to Cu_{(s)}$
Je höher die Konzentration der Kupfersulfat-Lösung, desto größer die Wahrscheinlichkeit, dass die überschüssigen Elektronen der Kupfer-Elektrode von Kupfer-Ionen aufgenommen werden können.
Damit ist unser kleiner chemischer Exkurs beendet, und wir kommen nun zum eigentlichen Thema dieses Artikels, nämlich der Nerst-Gleichung, wie sie für die Berechnung des Membranpotenzials einer Nervenzelle wichtig ist.
Berechnung des Membranpotenzials
Der folgende Abschnitt geht davon aus, dass Sie die Grundlagen der Entstehung des Ruhepotenzials gelesen und verstanden haben. Falls nicht, bitte ganz schnell nachholen, sonst verstehen Sie nichts von den folgenden Ausführungen!
Das K+-Gleichgewichtspotenzial
Angenommen, nur die Kalium-Ionen spielen für die Entstehung des Membranpotenzials eine Rolle, so dass wir den Einfluss der Natrium-, Chlorid- und organischen Anionen ignorieren können. Dann würden solange K+-Ionen nach außen strömen, bis das sich bildende elektrische Potenzial genau so groß ist wie der langsam geringer werdende Diffusionsdruck bzw. das chemische K+-Potenzial. Es hat sich dann ein elektrochemisches Gleichgewicht zwischen chemischem und elektrischem Potenzial eingestellt, pro Zeiteinheit diffundieren genau so viele K+-Ionen nach außen wie nach innen. Das elektrische Potenzial, dass dann an der Membran gemessen werden kann, wird als K+-Gleichgewichtspotenzial bezeichnet.
Mit der Nernst-Gleichung kann man dieses K+-Gleichgewichtspotenzial nun berechnen:
$E_{K} = \frac{R*T}{F} * \ log(\frac{K^{+}_{außen}}{K^{+}_{innen}})$R ist dabei die sogenannte Gaskonstante, T die absolute Temperatur, gemessen in Kelvin und F die Faradaykonstante. $K^{+}_{außen}$ und $K^{+}_{innen}$ sind die Konzentrationen der Kalium-Ionen im Außenmedium und im Innern der Nervenzelle.
Bei einer Temperatur von 37 ºC, wie sie beispielsweise in menschlichen Zellen herrscht, vereinfacht sich der Ausdruck zu
$E_{K} = -61mV \ * \ log(\frac{K^{+}_{innen}}{K^{+}_{außen}})$
Achtung: Außen und innen sind jetzt vertauscht, dafür wurde der $\frac{R*T}{F}$-Term mit einem negativen Vorzeichen versehen.
Schauen wir uns jetzt mal die Konzentrationsverhältnisse an/in einer menschlichen Nervenzelle an. Im Zellplasma der Nervenzelle herrscht eine Konzentration von ca. 155 mmol/l, im Außenmedium eine Konzentration von 4 mmol/l [1]. Setzen wir diese Wert mal in die vereinfachte Nernst-Gleichung ein, dann erhalten wir
$E_{K} = -61mV \ * \ log(\frac{155\ mol/l}{4 \ mol/l})$
Als Ergebnis erhalten wir dann -96,88 mV. Das ist das Gleichgewichts-Kaliumpotenzial. Und dieser Wert wäre auch das Ruhepotenzial der menschlichen Nervenzelle, wenn das Ruhepotenzial ausschließlich von der Kalium-Diffusion abhängen würde.
Das tatsächliche Ruhepotenzial menschlicher Nervenzellen liegt aber bei -70 mV.
Das Na+-Gleichgewichtspotenzial
Das Ruhepotenzial einer Säugetier-Nervenzelle ist nicht ganz so "groß" wie das berechnete K+-Gleichgewichtspotenzial. Das K+-Gleichgewichtspotenzial wurde durch Ausströmen positiver Ladungen bewirkt. Wenn das tatsächliche Membranpotenzial nun etwas schwächer ist, könnte man das auf zwei Weisen erklären:
- Entweder strömen andere positive Ladungen in die Zelle ein
- oder es strömen zusätzlich negative Ladungen aus der Zelle aus.
Den zweiten Fall können wir ausschließen. In der Zelle gibt es zwar Chlorid-Ionen, jedoch ist deren Konzentration verschwindend klein, so dass sie keine Rolle spielen dürften. Und dann gibt es da noch die großen organischen Anionen. Diese sind aber zu groß, als dass sie die Membran passieren können. Also können wir diese negativen Ladungen auch vergessen. Es bleibt nur noch die erste Möglichkeit, nämlich das Einströmen von positiven Ladungen. Hier kämen Calcium-Ionen und Natrium-Ionen in Frage, die beide in recht hoher Konzentration im Außenmedium vorhanden sind. Aber wie man herausgefunden hat, spielen die Calcium-Ionen Ca2+ auch eine eher untergeordnete Rolle beim Membranpotenzial. Also bleiben nur noch die Natrium-Ionen Na+.
Das Natrium-Gleichgewichtspotenzial für T = 37 ºC berechnet sich ähnlich wie das Kalium-Gleichgewichtspotenzial:
$$E_{K} = -61mV \ * \ log(\frac{Na^{+}_{innen}}{Na^{+}_{außen}})$$
Wenn wir wieder die Werte aus [1] einsetzen, erhalten wir
$E_{K} = -61mV \ * \ log(\frac{12 \ mol/l}{145 \ mol/l})$
Daraus berechnet sich dann das Na+-Gleichgewichtspotenzial mit +67,1 mV.
In das tatsächliche Ruhepotenzial einer Nervenzelle fließt also zu einem geringen Anteil auch das Na+-Gleichgewichtspotenzial mit ein.
Experimenteller Beleg für den Einfluss der Na+-Ionen
Wenn man die Na+-Ionen im Außenmedium durch größere Kationen ersetzt, die auf gar keinen Fall durch die Zellmembran passen, dann stellt sich ein Ruhepotenzial ein, das in etwa dem K+-Gleichgewichtspotenzial entspricht. Cholin+ ist beispielsweise ein solches Kation [2].
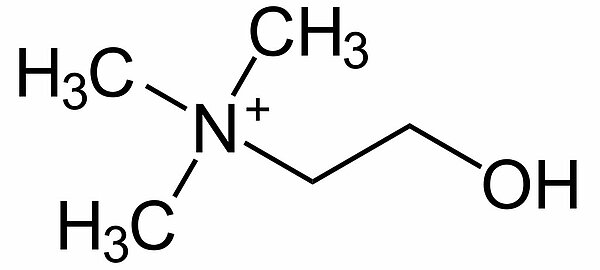
Der Einfluss der Membranpermeabilitäten
Einen wichtigen Einfluss auf das Membranpotenzial spielen die Permeabilitäten der Membran für die verschiedenen Ionensorten. Setzt man die Permeabilität für Kalium-Ionen auf den willkürlichen Wert 1, so haben Chlorid-Ionen eine relative Permeabilität von 0,45 und Natrium-Ionen eine relative Permeabilität von 0,04. Berücksichtig man diese Werte, dann kommt man zu der Goldmann-Gleichung, mit der man das Membranpotenzial in Abhängigkeit von den drei genannten Ionensorten berechnen kann:
$E_{Membran} = \frac{R\cdot T}{F} \cdot \ log(\frac{P_{K}\cdot K^{+}_{a} + P_{Na}\cdot Na^{+}_{a} + P_{Cl}\cdot Cl^{+}_{a}} {P_{K}\cdot K^{+}_{i} + P_{Na}\cdot Na^{+}_{i} + P_{Cl}\cdotp Cl^{+}_{i}})$Beim Einsetzen der Werte muss man jetzt allerdings aufpassen. In [2] werden für die Permeabilitäten völlig von [1] abweichende Werte eingesetzt, nämlich PNa=1, PK=20 und PCl = 0,1. Der Wert für die Chlorid-Permeabilität ist allerdings recht ungewöhnlich. Sollte da bei [2] etwa ein Fehler aufgetreten sein?
$E_{Membran} = \frac{R\cdot T}{F} \cdot \ log(\frac{237} {3112}) = 61 mV \cdot -0,39 = 68,2 mV$
Dieser theoretische Wert stimmt ziemlich gut mit dem gemessenen Wert des Säugetier-Membranpotenzials im Ruhezustand überein.
Anmerkung:
Die Frage nach den tatsächlichen Membranpermeabilitäten steht noch im Raum. Zwei wichtige Quellen [1] und [2] unterscheiden sich erheblich. Da ist mal eine genauere Recherche in der Fachliteratur notwendig.

Toll, als erstes werden meine eigenen Seiten bei Google genannt, also scheine ich ja die totale Kapazität in Sachen Membranpermeabilität zu sein.
Im Lexikon der Biologie des Spektrum-Verlags findet man die gleichen Permeabilitäten wie in [1]:
"Die Permeabilitätskonstanten der 3 Ionenarten verhalten sich in etwa PK: PCl: PNa = 1 : 0,45 : 0,04." [3]
In einem Skript der Uni München werden für die Permeabilitäten im Ruhezustand folgende Werte angegeben: PK = 15, PNa = 1, PCl = 1. Wenn man die Kalium-Permeabilität auf 1 setzt, ergeben sich diese Werte: PKK = 1, PNa = 0,07, PCl = 0,07 [4].
In dem Buch von Shepherd [5] finden sich wieder die Permeabilitäts-Wert von Schmidt.
Quellen:
- Schmidt: Grundriß der Neurophysiologie, Berlin Heidelberg 1987
- Dudel, Menzel, Schmidt: Neurowissenschaft, Heidelberg 2001.
- Lexikon der Biologie, Spektrum-Verlag 1999, Stichwort "Membranpotenzial".
- Skript zur Vorlesung Biophysik (WS 03/04) der Uni München
- Shepherd: Neurobiologie, Berlin Heidelberg 1993.