Vorbemerkung
Das DALTONsche Atommodell von 1803 ist nicht das erste Atommodell, das Menschen erfunden haben. Die alten Griechen, vor allem LEUKIPP und sein Schüler DEMOKRIT (460 - 370 v. Chr.) waren ihrer Zeit damals weit voraus, auch sie dachten über Atommodelle nach, die aber heutigen wissenschaftlichen Ansprüchen nicht mehr genügen, darum breiten wir den Mantel des Schweigens um diese frühen Versuche einer atomaren Vorstellung aus (ich selbst habe sogar eine Philosophie-Prüfung zu diesem Thema abgelegt, also daher finde ich das Thema sehr interessant, aber leider gehört es nicht in den modernen Chemie-Unterricht, daher breche ich jetzt einfach mal mitten im…
Elemente
Nach DALTON (1766 - 1844) bestehen Elemente aus Atomen. Jedes Element besteht dabei aus einer eigenen Atomsorte. Da es über 105 Elemente gibt, existieren auch über 105 Atomsorten auf der Erde (Isotope sind dabei noch nicht mitgerechnet).
Atome sind nach der Vorstellung von DALTON extrem klein und kugelförmig. Sie haben eine bestimmte Größe und eine bestimmte Masse. Vor allem aber sind Atome unteilbar. Daher haben sie auch ihren Namen (griechisch atomos = unteilbar).
Das DALTONsche Atommodell
- Atome bestehen aus kleinen, massiven, unteilbaren Kugeln.
- Jedes Element besteht aus einer eigenen Atomsorte. Es gibt also genau soviele Atomsorten, wie es Elemente gibt.
- Jede Atomsorte hat einen bestimmten Radius und eine bestimmte Masse.
- Chemische Reaktionen sind Teilchengruppierungen: Bei einer Reaktion gruppieren sich die Atome der Ausgangsstoffe lediglich um. Weder werden Atome vernichtet, noch entstehen neue.
So primitiv wie das DALTON-Modell auch ist, man kann es immer noch gut verwenden, um zahlreiche Naturphänomene zu erklären. In den Chemiebüchern der 7. Klassen benutzt man das DALTON-Modell beispielsweise, um die Aggregatzustände der Stoffe zu erklären.
So würde John DALTON heutzutage einen winzigen Ausschnitt aus einem festen Element zeichnen, beispielsweise Magnesium:

Die Atome des Elements sind sehr regelmäßig angeordnet, man spricht heute auch von einer Gitterstruktur oder einer Kugelpackung. Ich weiß nicht, ob DALTON damals schon diese Fachbegriffe kannte bzw. verwendete, aber das ist ja auch unerheblich.
Und so würde DALTON, wenn er noch lebte, einen winzigen Ausschnitt aus einem flüssigen Element zeichnen, beispielsweise Quecksilber oder Brom bei Zimmertemperatur oder Schwefel bei 300 Grad Celcius:

Auch den gasförmigen Zustand könnte DALTON mit seinem Atommodell locker erklären: Die Atome hätten hier gar kleinen Zusammenhalt mehr, sie würden einzeln und mit hoher Geschwindigkeit durch den Raum flitzen.

Mit dem DALTONschen Kugelteilchenmodell kann man also sehr schön den Unterschied zwischen dem festen, dem flüssigen und dem gasförmigen Aggregatzustand erklären.
Gasförmige Elemente wie Sauerstoff, Stickstoff, Chlor etc., die in Form zweiatomiger Moleküle vorliegen, würde DALTON folgendermaßen darstellen:
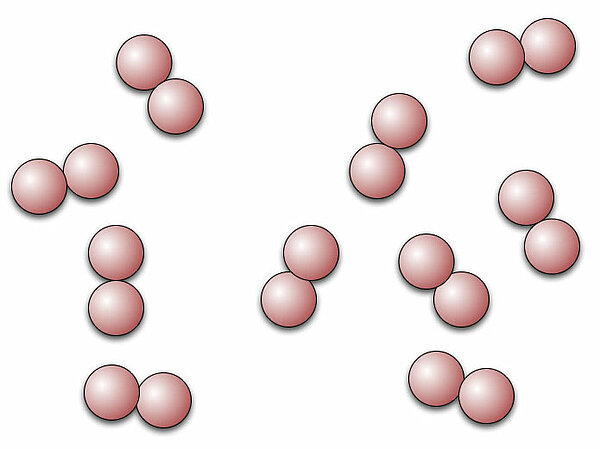
Verbindungen
Nach DALTON bestehen Verbindungen wie Wasser oder Zucker zwar auch aus Atomen, die Atome sind aber zu Molekülen organisiert. In den Schulbüchern drückt man das meistens so aus: Die kleinsten Teilchen einer Verbindung sind Moleküle, die aus mindestens zwei verschiedenen Atomen bestehen.
Sauerstoff besteht zwar auch aus Molekülen, aber jedes Sauerstoff-Molekül besteht aus zwei gleichen Atomen, nämlich zwei Sauerstoff-Atomen. Daher ist Sauerstoff ein Element und keine Verbindung.
Wasser dagegen ist eine typische Verbindung, denn die Wasser-Moleküle sind aus je einem Sauerstoff-Atom und zwei Wasserstoff-Atomen zusammengesetzt. Einen Ausschnitt aus flüssigem Wasser würde DALTON vielleicht so zeichnen:

Und schauen wir uns nun ein Gemisch aus Wasser und Brom an, so wie DALTON es zeichnen würde. Wasser ist eine Verbindung, während Brom ein Element ist, dessen kleinste Teilchen Moleküle aus je zwei Brom-Atomen sind.

Mit dem DALTONschen Atommodell kann man also gut die Existenz und die Eigenschaften von Stoffgemischen erklären - auch hierzu braucht man kein quantenmechanisches Atommodell.
Damit wären wir auch schon beim nächsten Punkt, der Leistungsfähigkeit des DALTONschen Atommodells.
Leistungsfähigkeit
Mit dem DALTONschen Atommodell kann man viele Phänomene der Natur erklären, man braucht dazu kein Schalenmodell oder gar Orbitalmodell. Ich kann hier nicht alle Phänomene aufzählen, die man mit dem DALTONschen Atommodell erklären kann, aber ein paar Beispiele möchte ich hier schon nennen.
Aggegatzustände und ZustandsänderungenAuf die Aggregatzustände bin ich bereits weiter oben eingegangen. Im festen Zustand befinden sich die Atome oder Moleküle in einer dichten Packung, daher sind feste Stoffe eben "fest" und haben eine hohe Dichte. Im flüssigen Zustand sind die kleinsten Teilchen (Atome oder Moleküle) recht locker angeordnet, berühren sich aber noch. Daher sind Flüssigkeiten "flüssig" und haben eine geringere Dichte. Im gasförmigen Zustand schließlich berühren sich die kleinsten Teilchen nicht mehr, sie flitzen mit hoher Geschwindigkeit durch den Raum. Dies erklärt die geringe Dichte eines Gases.
Ausdehnung von KörpernErhitzt man einen festen, flüssigen oder gasförmigen Körper, so dehnt sich dieser aus, weil sich die Abstände zwischen den Atomen oder Molekülen vergrößern.
Gesetz von der Erhaltung der MasseDieses bekannte Gesetz kann mit Hilfe der Atommassen leicht erklärt werden. Bei chemischen Reaktionen entstehen keine neuen Atome, noch gehen vorhandene Atome verloren. Die vorhandenen Atome der Ausgangsstoffe ordnen sich "lediglich" zu neuen Molekülen an, dabei geht natürlich keine Masse verloren.
Gesetz der konstanten Proportionen1 g Kupfer reagiert steht mit einer konstanten Menge Schwefel zu Kupfersulfid. 2 g Kupfer reagieren mit der doppelten Menge Schwefel, 10 g Kupfer mit der zehnfachen Menge und so weiter. Gebe ich zu viel Schwefel in das Gemisch der Ausgangsstoffe, bleibt am Ende Schwefel übrig, und gebe ich zu viel Kupfer in das Edukt-Gemisch, bleibt am Ende etwas Kupfer über. Auch dieses Phänomen kann man ohne Weiteres mit dem Atomlmodell von DALTON erklären.

9 Schwefel-Atome reagieren mit 22 Kupfer-Atomen zu 9 Kupfersulfid-"Molekülen" (sachlich nicht ganz korrekt, aber DALTON kannte noch keine Ionenverbindungen). Jedes Schwefel-Atom verbindet sich mit zwei Kupfer-Atomen. Vier Kupfer-Atome bleiben übrig.
Kupfer-Atome haben eine bestimmte Masse, und Schwefel-Atome haben eine bestimmte Masse. Kupfer- und Schwefel-Atome reagieren in einem bestimmten Zahlenverhältnis miteinander, nämlich 2 : 1, so dass man als "Summenformel" für die Verbindung Kupfersulfid Cu2S angeben kann. Angenommen, ein Cu-Atom "wiegt" 65 u (u ist die Masseneinheit der Atome) und ein S-Atom 32 u, und zwei Cu-Atome reagieren stets mit einem S-Atom, dann reagieren immer 130 u (nämlich 2 x 65 u) mit 32 u. Oder 130 Gramm Kupfer reagieren mit 32 Gramm Schwefel, oder 260 Gramm Kupfer reagieren mit 64 Gramm Schwefel und so weiter.
VolumenreduktionDiesen Versuch führe ich immer im Unterricht der Klasse 7 durch, die Schüler sind stets beeindruckt. Man misst sehr genau 50 ml Wasser und 50 ml Ethanol in zwei verschiedenen Messzylindern ab, dann mischt man die beiden Reinstoffe in einem 100 ml - Messzylinder. Und jetzt geschieht das Unglaubliche: Man hat am Ende nur 97 oder 98 ml Stoffgemisch! Wo ist der Rest gebieben?
Diese Volumenreduktion kann man ganz leicht mit dem Kugelteilchenmodell von DALTON erklären.

Wasser und Alkohol bestehen aus Molekülen, diese sind wiederum aus Atomen zusammengesetzt. Da die Alkohol-Moleküle aus wesentlich mehr Atomen bestehen als die Wasser-Moleküle, sind sie auch viel größer. Das Mischen von Alkohol und Wasser kann man recht schön mit Erbsen und Senfkörnern veranschaulichen. Die Senfkörner verschwinden fast komplett in den Lücken zwischen den Erbsen, und auf analoge Weise verschwinden die Wasser-Moleküle in den Lücken zwischen den Alkohol-Molekülen. Natürlich nicht ganz so extrem wie die Senfkörner, schließlich gehen ja nur ein paar Prozent des Volumens verloren.
Dies waren nur fünf Beispiele für Phänomene aus dem Alltag oder dem Chemielabor, die man sehr einfach mit dem DALTONschen Atommodell erklären kann. Und das sollte man auch tun. Um Schülern oder anderen Leuten die Volumenreduktion oder das Gesetz von der Erhaltung der Masse zu erklären, brauche ich kein Orbitalmodell oder Kugelwolkenmodell, sondern das DALTONsche Atommodell reicht völlig aus.