
Dieser Screenshot zeigt vier verschiedene Ausgabe des 21-Städte-Problems. Jedes Mal wurde eine andere Anfangsstadt gewählt. Dazu musste die Methode nearestneighbour leicht umgeschrieben werden:
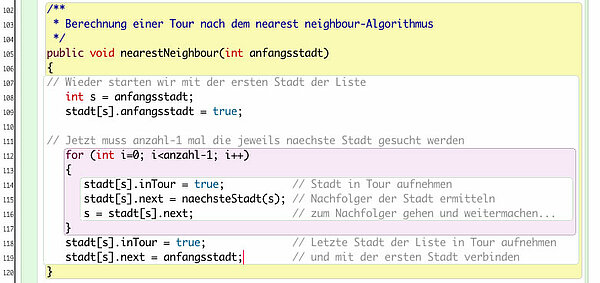
Die Klasse Stadt wurde um ein boolean-Attribut anfangsstadt erweitert, so dass die erste Stadt der Tour im Applet grün gezeichnet werden kann.
Man kann an den vier Screenshots gut erkennen, dass die erste Tour mit der Anfangsstadt 0 (Bohmte) tatsächlich noch verbessert werden kann. Die Tour mit der Anfangsstadt Lübbecke sieht viel kürzer aus.
Also besteht die Optimierung des nearest neighbour-Algorithmus darin, dass man nacheinander jede Stadt zur Anfangsstadt macht und dann die kürzeste ermittelte Route als Tour nimmt.
Dazu braucht man eine Methode gesamtlaenge, welche die Gesamtlänge einer Tour ermittelt. Eine solche Methode ist schnell geschrieben.

Dann brauchen wir eine Methode, die alle möglichen Touren ausprobiert und dann die kürzeste Tour von allen möglichen ermittelt:
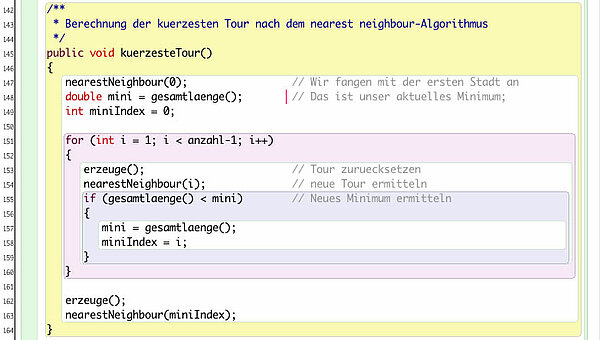
Schon ist das Problem gelöst und wir finden eine recht kurze Tour:
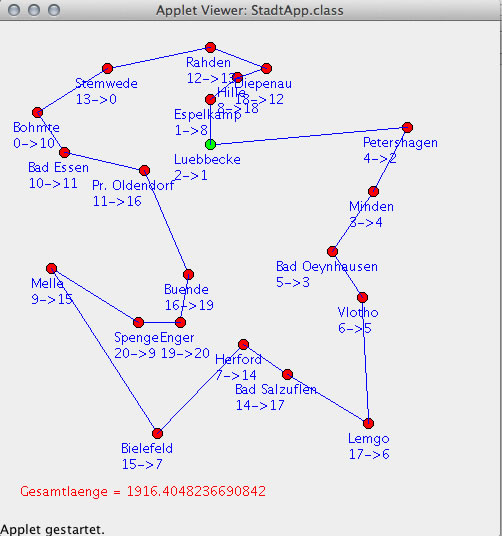
Dies ist die kürzeste Tour, die nach dem nearest neighbour-Algorithmus möglich ist.
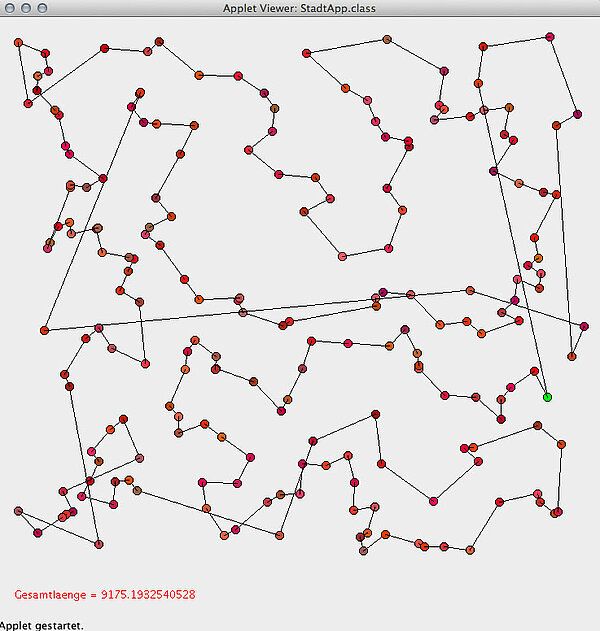
Hier wurde der optimierte Algorithmus auf 200 Zufallstädte (x- und y-Position wurden zufällig generiert) angewandt, das Ergebnis ist ganz passabel.
Auf der nächsten Seite stelle ich einen von Sedgewick erarbeiteten Algorithmus vor, mit dem Überschneidungen in der Tour entfernt werden können, was zu einer weitern Optimierung der Rundreise führt.