Dieses Thema ist für Abiturienten im Fach Informatik von besonderem Interesse. Für den Abiturjahrgang 2019 schreiben die Vorgaben des Landes NRW das Thema "nichtdeterminierte endliche Automaten" vor. Daher habe ich spontan diese Seite über NDEAs bzw. nichtdeterminierte endliche Automaten geschrieben.
Definition
Nichtdeterminierter endlicher Automat (NDEA oder auch NEA)
Ein nichtdeterminierter endlicher Automat (DEA) ist ein 5-Tupel A = (Q, S, δ, q0, F) mit
- Q = endliche Menge von Zuständen
- S = Eingabealphabet
- δ = Übergangsfunktion
- q0 = Startzustand
- F = endliche Menge von Endzuständen.
Auf den ersten Blick sieht diese Definition genau so aus wie die Definition eines determinierten endlichen Automaten. Auf den zweiten Blick auch. Das liegt daran, dass die Definition keine näheren Angaben macht, wie die Übergangsfunktion auszusehen hat.
Bei einem DEA weist die Übergangsfunktion jedem Zustand und jedem Eingabezeichen genau einen Folgezustand zu. Bei einem NDEA ist das etwas anders. Hier kann die Übergangsfunktion einem Zustand und einem Eingabezeichen mehr als einen Folgezustand zuweisen. Schauen wir uns das mal konkret an einem einfachen Beispiel an:
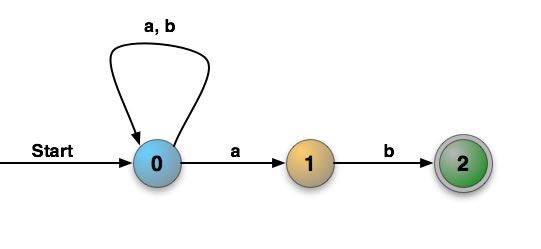
Aus dem Startzustand 0 gelangt man mit dem Zeichen 'a' in den Zustand 1 und gleichzeitig auch zurück in den Zustand 0. Das ist so ähnlich wie die Sache mit Schrödingers Katze. Wenn sich der Automat im Zustand 0 befindet und dann das Zeichen 'a' kommt, kann man nicht sehen, in welchem Folgezustand sich der Automat befindet. Er könnte sich im Zustand 1 befinden, aber auch im Zustand 0.
Wir wollen diesen NDEA nun formal definieren (so etwas wird auch immer wieder in den Abituraufgaben verlangt).
Zustandsmenge Q
Q = {0, 1, 2}
Eingabealphabet S
S = {a, b}
Übergangsfunktion δ
siehe Abbildung 1
Startzustand q0
q0 = 0
Endzustände F
F = {2}
In Abituraufgaben wird auch immer wieder verlangt, die Übergangsfunktion in Form einer Tabelle darzustellen. Auch das wollen wir hier machen.
| Zustand | Eingabesymbol a | Eingabesymbol b |
| 0 | 0, 1 | 0 |
| 1 | --- | 2 |
| 2 | --- | --- |
Umwandlung eines NDEA in einen DEA
Auch hier kann man eine Tabelle verwenden. Diese Tabelle wollen wir Schritt für Schritt konstruieren. Wir beginnen im Zustand 0 und fragen uns, in welche Folgezustände kann der NEA gelangen, wenn das Zeichen 'a' gelesen wird? Die obige Tabelle sagt uns eindeutig: Die Folgezustände sind 0 und 1. Wenn im Zustand 0 dagegen das Zeichen 'b' gelesen wird, gelangen wir zurück in den Zustand 0. Aber das konnte man ja auch schon der obigen Tabelle entnehmen:
| Zustand | Eingabesymbol a | Eingabesymbol b |
| 0 | 0, 1 | 0 |
| 1 | --- | 2 |
| 2 | --- | --- |
Jetzt kommt etwas Neues. Wir betrachten die Situation, dass sich der Automat gleichzeitig in den Zuständen 0 und 1 befindet, als neuen "Superzustand", den wir als {0,1} bezeichnen. Die Mengen-Notation deutet an, dass es sich um eine Menge von Zuständen handelt.
Der Automat befindet sich jetzt im Superzustand {0,1}. Was passiert, wenn nun das Zeichen 'a' gelesen wird? Wie wie reagiert der Automat, wenn das Zeichen 'b' erkannt wird?
Dazu können wir wieder die erste Tabelle benutzen. Wir markieren jetzt einfach die beiden Zeilen für die Zustände 0 und 1:
| Zustand | Eingabesymbol a | Eingabesymbol b |
| 0 | 0, 1 | 0 |
| 1 | --- | 2 |
| 2 | --- | --- |
Und dann können wir regelrecht "sehen", was passiert. Mit dem Eingabesymbol 'a' gelangen wir erneut in den Superzustand {0,1}, und mit dem Eingabesymbol 'b' erreichen wir einen neuen Superzustand, nämlich {0,2}.
Nun untersuchen wir, was im Superzustand {0,2} so alles passieren kann. Dazu markieren wir die ursprüngliche Tabelle entsprechend:
| Zustand | Eingabesymbol a | Eingabesymbol b |
| 0 | 0, 1 | 0 |
| 1 | --- | 2 |
| 2 | --- | --- |
Mit dem Symbol 'a' gelangen wir wieder in den Superzustand {0,1}, und mit dem Symbol 'b' geht es in den Zustand 0. Fassen wir nun diese Erkenntnisse in einer neuen Tabelle zusammen:
| Zustand | Eingabesymbol a | Eingabesymbol b |
| {0} | {0, 1} | {0} |
| {0, 1} | {0, 1} | {0, 2} |
| {0, 2} | {0, 1} | {0} |
Diese Tabelle können wir nun wieder als Übergangsfunktion eines determinierten endlichen Automaten ansehen und graphisch darstellen:
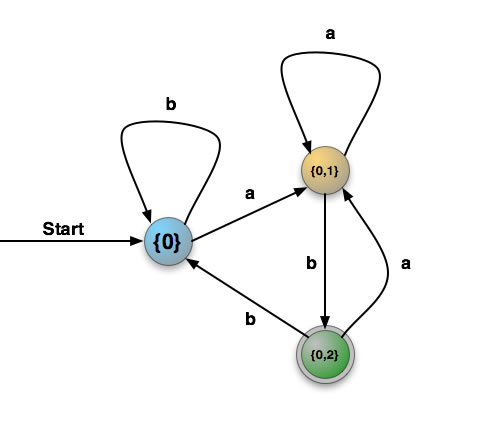
Die Zustandsmenge {0, 2} ist ein Endzustand, weil sie den "alten" Endzustand 2 des nichtdeterminierten endlichen Automaten enthält.
Ein weiteres Beispiel
Betrachten Sie nun folgenden NEA, der alle Ziffernfolgen akzeptiert, die auf 007 enden. Die Idee zu diesem DEA kommt natürlich wieder aus einer alten NRW-Abituraufgabe.
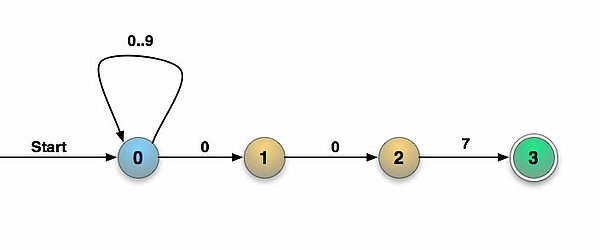
Beginnen wir gleich mit der Konstruktion der Teilmengen bzw. "Superzustände". Es ergibt sich damit folgende Tabelle:
| Zustand | 1,2,3,4,5,6, 8,9 | Eingabesymbol 0 | Eingabesymbol 7 |
| {0} | {0} | {0, 1} | {0} |
| {0, 1} | {0} | {0, 2} | {0} |
| {0, 2} | {0} | {0, 1} | {0, 3} |
| {0, 3} | {0} | {0, 1} | {0} |
Bei dieser Tabellenkonstruktion muss man sich ziemlich konzentrieren, Fehler werden hier ganz schnell gemacht, wenn man nicht aufpasst. Setzen wir diese Tabelle nun wieder in eine Graphik um.
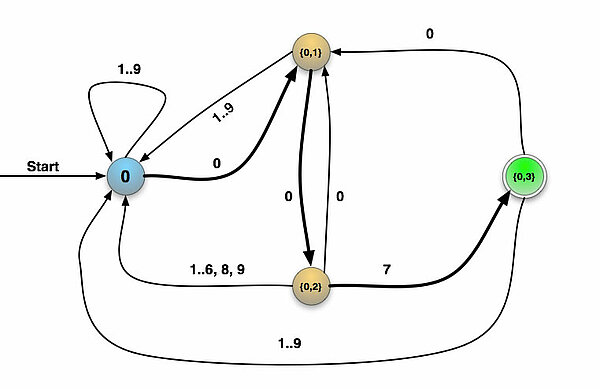
Die Zahl der Zustände hat sich gegenüber dem NEA nicht vergrößert, wohl aber die Zahl der Übergänge. Wir wollen nun anhand einiger Beispiele testen, ob der DEA tatächlich nur Ziffernfolgen akzeptiert, die auf 007 enden.
Probieren wir zunächst einmal - ganz radikal - die Ziffernfolge 007, die ja auch auf 007 endet. Mit der 0 gelangen wir von Zustand 0 in den Zustand {0,1}, mit der zweiten 0 in den Zustand {0,2} und mit der 7 in den Endzustand 3. Die Ziffernfolge 007 wird also von dem Automaten akzeptiert.
Nun denken wir uns mal eine beliebige auf 007 endende Ziffernfolge aus, beispielsweise 1436237400752007.
Das ist jetzt eine ziemlich lange "zufällige" Ziffernfolge. Mit den ersten acht Ziffern 14362374 bleiben wir stets im Zusand 0. Dann kommt die erste 0, die uns in den Zustand {0,1} führt. Mit der zweiten 0 geht es in den Zustand {0,2} und mit der 7 in den Zustand {0,3}. Dann kommen aber weitere Ziffern. Die 5 bringt uns in den Zustand 0, mit der 2 bleiben wir in Zustand 0. Nun kommt wieder die Ziffernfolge 007, die uns in den Endzustand {0,3} bringt. Die Ziffernfolge ist fertig abgearbeitet, der DEA befindet sich in einem Endzustand, also gilt die Ziffernfolge als akzeptiert.
Sinn und Nutzen von NEAs
Einen DEA kann man direkt in eine Tabelle umsetzen und diese dann leicht implementieren, so dass man eine Methode schreiben kann, die einen DEA simuliert. Bei einem NEA geht das nicht, weil sich ein NEA gleichzeitig in mehreren Zuständen befinden kann. Warum beschäftigt man sich dann überhaupt mit NEAs?
Wie wir bei unseren beiden Beispielen gesehen haben, ist ein NEA wesentlich einfacher aufgebaut als ein äquivalenter DEA. "Äquivalenz" heißt hier, dass der DEA die gleiche Sprache hat wie der NEA. Einen NEA kann man schneller und einfacher konstruieren als den äquivalenten DEA. Hat man einen NEA konstruiert, kann mit Hilfe des hier vorgestellten Teilmengen-Algorithmus leicht ein äquivalenter DEA konstruiert werden, den man dann wieder leicht implementieren kann.
Implementation eines NEAs
Man kann versuchen, einen NEA zu implementieren. Nehmen wir als Beispiel den 007-NEA aus Abbildung 3. Wenn wir uns die Tabelle mit den Teilmengen bzw. Superzuständen anschauen, erkennen wir, dass der NEA maximal zwei Zustände gleichzeitig einnehmen kann, zum Beispiel {0, 1}. Also müsste man diesen speziellen NEA doch leicht implementieren können, indem man einfach zwei Zustandsvariablen verwaltet.
Hier der entsprechende Java-Quelltext:
public class NDEA007
{
int zustand1, zustand2;
public NDEA007()
{
zustand1 = 0; zustand2 = 0;
}
private boolean isNumber(int c)
{
return ((0 <= c) && (c <= 9));
}
public void nextStep(int c)
{
if ((zustand1 == 0) && isNumber(c)) // Bedingung 1
zustand1 = 0;
if ((zustand2 == 0) && (c == 0)) // Bedingung 2
zustand2 = 1;
else if ((zustand2 == 1) && (c == 0)) // Bedingung 3
zustand2 = 2;
else if ((zustand2 == 2) && (c == 7)) // Bedingung 4
zustand2 = 3;
if (zustand2 == zustand1)
System.out.println("Der NDEA befindet sich in dem Zustand "+ zustand1 + ".");
else
System.out.println("Der NDEA befindet sich in den Zuständen "+
zustand1 + " und " + zustand2 + ".");
}
}Ich denke, dieser Quelltext muss nicht weiter kommentiert werden, da er sehr einfach zu verstehen ist. Das liegt daran, dass der NEA nur vier Zustände hat und sich maximal in nur zwei Zuständen gleichzeitig aufhalten kann.
Was wäre aber, wenn der NEA komplexer ist, beispielsweise 10 Zustände hat und er sich gleichzeitig in drei, vier oder mehr Zuständen aufhalten kann?
In diesem Fall würde man nicht zwei Variablen zustand1 und zustand2 anlegen, sondern einen Array oder eine Liste von Zuständen, und schon wäre das Problem gelöst.